Public Member Functions | Static Public Member Functions | Private Member Functions | Private Attributes | Static Private Attributes | List of all members
genf::GFMaterialEffects Class Reference

#include <GFMaterialEffects.h>

Inheritance diagram for genf::GFMaterialEffects:

Public Member Functions

void setEnergyLossBetheBloch (bool opt=true)
 
void setNoiseBetheBloch (bool opt=true)
 
void setNoiseCoulomb (bool opt=true)
 
void setEnergyLossBrems (bool opt=true)
 
void setNoiseBrems (bool opt=true)
 
double effects (const std::vector< TVector3 > &points, const std::vector< double > &pointPaths, const double &mom, const int &pdg, const bool &doNoise=false, TMatrixT< Double_t > *noise=NULL, const TMatrixT< Double_t > *jacobian=NULL, const TVector3 *directionBefore=NULL, const TVector3 *directionAfter=NULL)
 Calculates energy loss in the travelled path, optional calculation of noise matrix. More...
 
double stepper (const double &maxDist, const double &posx, const double &posy, const double &posz, const double &dirx, const double &diry, const double &dirz, const double &mom, const int &pdg)
 Returns maximum length so that a specified momentum loss will not be exceeded. More...
 
double stepper (const double &maxDist, const TVector3 &pos, const TVector3 &dir, const double &mom, const int &pdg)
 

Static Public Member Functions

static GFMaterialEffects * getInstance ()
 
static void destruct ()
 

Private Member Functions

 GFMaterialEffects ()
 
virtual ~GFMaterialEffects ()
 
void getParameters ()
 contains energy loss classes More...
 
void calcBeta (double mom)
 sets fbeta, fgamma, fgammasquare; must only be used after calling getParameters() More...
 
double energyLossBetheBloch (const double &mom)
 Returns energy loss. More...
 
void noiseBetheBloch (const double &mom, TMatrixT< double > *noise) const
 calculation of energy loss straggling More...
 
void noiseCoulomb (const double &mom, TMatrixT< double > *noise, const TMatrixT< double > *jacobian, const TVector3 *directionBefore, const TVector3 *directionAfter) const
 calculation of multiple scattering More...
 
double energyLossBrems (const double &mom) const
 Returns energy loss. More...
 
void noiseBrems (const double &mom, TMatrixT< double > *noise) const
 calculation of energy loss straggeling More...
 
double MeanExcEnergy_get (int Z)
 
double MeanExcEnergy_get (TGeoMaterial *)
 

Private Attributes

bool fEnergyLossBetheBloch
 
bool fNoiseBetheBloch
 
bool fNoiseCoulomb
 
bool fEnergyLossBrems
 
bool fNoiseBrems
 
const double me
 
double fstep
 
double fbeta
 
double fdedx
 
double fgamma
 
double fgammaSquare
 
double fmatDensity
 
double fmatZ
 
double fmatA
 
double fradiationLength
 
double fmEE
 
int fpdg
 
double fcharge
 
double fmass
 

Static Private Attributes

static GFMaterialEffects * finstance = NULL
 

Detailed Description

Definition at line 50 of file GFMaterialEffects.h.

Constructor & Destructor Documentation

genf::GFMaterialEffects::GFMaterialEffects ( )
private

Definition at line 56 of file GFMaterialEffects.cxx.

56  :
57  fEnergyLossBetheBloch(true), fNoiseBetheBloch(true),
58  fNoiseCoulomb(true),
59  fEnergyLossBrems(true), fNoiseBrems(true),
60  me(0.510998910E-3),
61  fstep(0),
62  fbeta(0),
63  fdedx(0),
64  fgamma(0),
65  fgammaSquare(0),
66  fmatDensity(0),
67  fmatZ(0),
68  fmatA(0),
69  fradiationLength(0),
70  fmEE(0),
71  fpdg(0),
72  fcharge(0),
73  fmass(0) {
74 }
genf::GFMaterialEffects::~GFMaterialEffects ( )
privatevirtual

Definition at line 40 of file GFMaterialEffects.cxx.

40  {
41  // for(unsigned int i=0;i<fEnergyLoss.size();++i) delete fEnergyLoss.at(i);
42  //delete geoMatManager;
43 }

Member Function Documentation

void genf::GFMaterialEffects::calcBeta ( double  mom)
private

sets fbeta, fgamma, fgammasquare; must only be used after calling getParameters()

Definition at line 276 of file GFMaterialEffects.cxx.

276  {
277  fbeta = mom/sqrt(fmass*fmass+mom*mom);
278 
279  //for numerical stability
280  fgammaSquare = 1.-fbeta*fbeta;
281  if(fgammaSquare>1.E-10) fgammaSquare = 1./fgammaSquare;
282  else fgammaSquare = 1.E10;
283  fgamma = sqrt(fgammaSquare);
284 }
void genf::GFMaterialEffects::destruct ( )
static

Definition at line 81 of file GFMaterialEffects.cxx.

81  {
82  if(finstance != NULL) {
83  delete finstance;
84  finstance = NULL;
85  }
86 }
genf::GFMaterialEffects::finstance
static GFMaterialEffects * finstance
Definition: GFMaterialEffects.h:55
double genf::GFMaterialEffects::effects ( const std::vector< TVector3 > &  points,
const std::vector< double > &  pointPaths,
const double &  mom,
const int &  pdg,
const bool &  doNoise = false,
TMatrixT< Double_t > *  noise = NULL,
const TMatrixT< Double_t > *  jacobian = NULL,
const TVector3 *  directionBefore = NULL,
const TVector3 *  directionAfter = NULL 
)

Calculates energy loss in the travelled path, optional calculation of noise matrix.

Definition at line 88 of file GFMaterialEffects.cxx.

96  {
97 
98  //assert(points.size()==pointPaths.size());
99  fpdg = pdg;
100 
101  double momLoss=0.;
102 
103  for(unsigned int i=1;i<points.size();++i){
104  // TVector3 p1=points.at(i-1);
105  //TVector3 p2=points.at(i);
106  //TVector3 dir=p2-p1;
107  TVector3 dir=points.at(i)-points.at(i-1);
108  double dist=dir.Mag();
109  double realPath = pointPaths.at(i);
110 
111  if (dist > 1.E-8) { // do material effects only if distance is not too small
112  dir*=1./dist; //normalize dir
113 
114  double X(0.);
115  /*
116  double matDensity, matZ, matA, radiationLength, mEE;
117  double step;
118  */
119 
120  gGeoManager->InitTrack(points.at(i-1).X(),points.at(i-1).Y(),points.at(i-1).Z(),
121  dir.X(),dir.Y(),dir.Z());
122 
123  while(X<dist){
124 
125  getParameters();
126  // geoMatManager->getMaterialParameters(matDensity, matZ, matA, radiationLength, mEE);
127 
128  // step = geoMatManager->stepOrNextBoundary(dist-X);
129  gGeoManager->FindNextBoundaryAndStep(dist-X);
130  fstep = gGeoManager->GetStep();
131 
132  // Loop over EnergyLoss classes
133  if(fmatZ>1.E-3){
134  /*
135  for(unsigned int j=0;j<fEnergyLoss.size();++j){
136  momLoss += realPath/dist*fEnergyLoss.at(j)->energyLoss(step,
137  mom,
138  pdg,
139  matDensity,
140  matZ,
141  matA,
142  radiationLength,
143  mEE,
144  doNoise,
145  noise,
146  jacobian,
147  directionBefore,
148  directionAfter);
149  }
150  */
151  calcBeta(mom);
152 
153  if (fEnergyLossBetheBloch)
154  momLoss += realPath/dist * this->energyLossBetheBloch(mom);
155  if (doNoise && fEnergyLossBetheBloch && fNoiseBetheBloch)
156  this->noiseBetheBloch(mom, noise);
157 
158  if (/*doNoise &&*/ fNoiseCoulomb) // Force it
159  this->noiseCoulomb(mom, noise, jacobian, directionBefore, directionAfter);
160 
161  if (fEnergyLossBrems)
162  momLoss += realPath/dist * this->energyLossBrems(mom);
163  if (doNoise && fEnergyLossBrems && fNoiseBrems)
164  this->noiseBrems(mom, noise);
165 
166 
167 
168  }
169 
170  X += fstep;
171 
172  }
173  }
174  }
175  //std::cout << "GFMaterialEffects::effects(): momLoss " << momLoss << std::endl;
176  return momLoss;
177 }
genf::GFMaterialEffects::noiseBrems
void noiseBrems(const double &mom, TMatrixT< double > *noise) const
calculation of energy loss straggeling
Definition: GFMaterialEffects.cxx:646
genf::GFMaterialEffects::noiseCoulomb
void noiseCoulomb(const double &mom, TMatrixT< double > *noise, const TMatrixT< double > *jacobian, const TVector3 *directionBefore, const TVector3 *directionAfter) const
calculation of multiple scattering
Definition: GFMaterialEffects.cxx:390
genf::GFMaterialEffects::energyLossBrems
double energyLossBrems(const double &mom) const
Returns energy loss.
Definition: GFMaterialEffects.cxx:484
genf::GFMaterialEffects::noiseBetheBloch
void noiseBetheBloch(const double &mom, TMatrixT< double > *noise) const
calculation of energy loss straggling
Definition: GFMaterialEffects.cxx:327
dir
string dir
Definition: INukeNucleonCorr.cxx:61
genf::GFMaterialEffects::calcBeta
void calcBeta(double mom)
sets fbeta, fgamma, fgammasquare; must only be used after calling getParameters() ...
Definition: GFMaterialEffects.cxx:276
larg4::dist
constexpr double dist(const TReal *x, const TReal *y, const unsigned int dimension)
Definition: OpFastScintillation.hh:563
run_cnn_1class.pdg
pdg
Definition: run_cnn_1class.py:54
genf::GFMaterialEffects::getParameters
void getParameters()
contains energy loss classes
Definition: GFMaterialEffects.cxx:255
genf::GFMaterialEffects::energyLossBetheBloch
double energyLossBetheBloch(const double &mom)
Returns energy loss.
Definition: GFMaterialEffects.cxx:290
double genf::GFMaterialEffects::energyLossBetheBloch ( const double &  mom)
private

Returns energy loss.

Uses Bethe Bloch formula to calculate energy loss. Calcuates and sets fdedx which needed also for noiseBetheBloch. Therefore it is not a const function!

Definition at line 290 of file GFMaterialEffects.cxx.

290  {
291 
292  // calc fdedx, also needed in noiseBetheBloch!
293  fdedx = 0.307075*fmatZ/fmatA*fmatDensity/(fbeta*fbeta)*fcharge*fcharge;
294  double massRatio = me/fmass;
295  // me=0.000511 here is in GeV. So fmEE must come in here in eV to get converted to MeV.
296  double argument = fgammaSquare*fbeta*fbeta*me*1.E3*2./((1.E-6*fmEE) * sqrt(1+2*sqrt(fgammaSquare)*massRatio + massRatio*massRatio));
297 
298  if (fmass==0.0) return(0.0);
299  if (argument <= exp(fbeta*fbeta))
300  {
301  fdedx = 0.;
302  // so-called Anderson-Ziegler domain ... Let's approximate it with a flat
303  // 100 MeV/cm, looking at the muon dE/dx curve in the PRD Review, or, ahem, wikipedia.
304  // http://pdg.lbl.gov/2011/reviews/rpp2011-rev-passage-particles-matter.pdf
305  // But there's a practical problem: must not reduce momentum to zero for tracking in G3,
306  // so allow only 50% reduction of kinetic energy.
307  // fdedx = 100.0*1.E-3/fstep; // in GeV/cm, hence 1.e-3
308  //if (fdedx > 0.5*0.5*fmass*fbeta*fbeta/fstep) fdedx = 0.5*0.5*fmass*fbeta*fbeta/fstep;
309  }
310  else{
311  fdedx *= (log(argument)-fbeta*fbeta); // Bethe-Bloch [MeV/cm]
312  fdedx *= 1.E-3; // in GeV/cm, hence 1.e-3
313  if (fdedx<0.) fdedx = 0;
314  }
315 
316  double DE = fstep * fdedx; //always positive
317  double momLoss = sqrt(mom*mom+2.*sqrt(mom*mom+fmass*fmass)*DE+DE*DE) - mom; //always positive
318 
319  //in vacuum it can numerically happen that momLoss becomes a small negative number. A cut-off at 0.01 eV for momentum loss seems reasonable
320  if(fabs(momLoss)<1.E-11)momLoss=1.E-11;
321 
322  // if(fabs(momLoss)>mom)momLoss=mom; // For going fwd and ending its life. EC.
323  return momLoss;
324 }
double genf::GFMaterialEffects::energyLossBrems ( const double &  mom) const
private

Returns energy loss.

Can be called with any pdg, but only calculates energy loss for electrons and positrons (otherwise returns 0). Uses a gaussian approximation (Bethe-Heitler formula with Migdal corrections). For positrons the energy loss is weighed with a correction factor.

Definition at line 484 of file GFMaterialEffects.cxx.

484  {
485 
486  if (fabs(fpdg)!=11) return 0; // only for electrons and positrons
487 
488  #if !defined(BETHE)
489  static const double C[101]={ 0.0,-0.960613E-01, 0.631029E-01,-0.142819E-01, 0.150437E-02,-0.733286E-04, 0.131404E-05, 0.859343E-01,-0.529023E-01, 0.131899E-01,-0.159201E-02, 0.926958E-04,-0.208439E-05,-0.684096E+01, 0.370364E+01,-0.786752E+00, 0.822670E-01,-0.424710E-02, 0.867980E-04,-0.200856E+01, 0.129573E+01,-0.306533E+00, 0.343682E-01,-0.185931E-02, 0.392432E-04, 0.127538E+01,-0.515705E+00, 0.820644E-01,-0.641997E-02, 0.245913E-03,-0.365789E-05, 0.115792E+00,-0.463143E-01, 0.725442E-02,-0.556266E-03, 0.208049E-04,-0.300895E-06,-0.271082E-01, 0.173949E-01,-0.452531E-02, 0.569405E-03,-0.344856E-04, 0.803964E-06, 0.419855E-02,-0.277188E-02, 0.737658E-03,-0.939463E-04, 0.569748E-05,-0.131737E-06,-0.318752E-03, 0.215144E-03,-0.579787E-04, 0.737972E-05,-0.441485E-06, 0.994726E-08, 0.938233E-05,-0.651642E-05, 0.177303E-05,-0.224680E-06, 0.132080E-07,-0.288593E-09,-0.245667E-03, 0.833406E-04,-0.129217E-04, 0.915099E-06,-0.247179E-07, 0.147696E-03,-0.498793E-04, 0.402375E-05, 0.989281E-07,-0.133378E-07,-0.737702E-02, 0.333057E-02,-0.553141E-03, 0.402464E-04,-0.107977E-05,-0.641533E-02, 0.290113E-02,-0.477641E-03, 0.342008E-04,-0.900582E-06, 0.574303E-05, 0.908521E-04,-0.256900E-04, 0.239921E-05,-0.741271E-07,-0.341260E-04, 0.971711E-05,-0.172031E-06,-0.119455E-06, 0.704166E-08, 0.341740E-05,-0.775867E-06,-0.653231E-07, 0.225605E-07,-0.114860E-08,-0.119391E-06, 0.194885E-07, 0.588959E-08,-0.127589E-08, 0.608247E-10};
490  static const double xi=2.51, beta=0.99, vl=0.00004;
491  #endif
492  #if defined(BETHE) // no MIGDAL corrections
493  static const double C[101]={ 0.0, 0.834459E-02, 0.443979E-02,-0.101420E-02, 0.963240E-04,-0.409769E-05, 0.642589E-07, 0.464473E-02,-0.290378E-02, 0.547457E-03,-0.426949E-04, 0.137760E-05,-0.131050E-07,-0.547866E-02, 0.156218E-02,-0.167352E-03, 0.101026E-04,-0.427518E-06, 0.949555E-08,-0.406862E-02, 0.208317E-02,-0.374766E-03, 0.317610E-04,-0.130533E-05, 0.211051E-07, 0.158941E-02,-0.385362E-03, 0.315564E-04,-0.734968E-06,-0.230387E-07, 0.971174E-09, 0.467219E-03,-0.154047E-03, 0.202400E-04,-0.132438E-05, 0.431474E-07,-0.559750E-09,-0.220958E-02, 0.100698E-02,-0.596464E-04,-0.124653E-04, 0.142999E-05,-0.394378E-07, 0.477447E-03,-0.184952E-03,-0.152614E-04, 0.848418E-05,-0.736136E-06, 0.190192E-07,-0.552930E-04, 0.209858E-04, 0.290001E-05,-0.133254E-05, 0.116971E-06,-0.309716E-08, 0.212117E-05,-0.103884E-05,-0.110912E-06, 0.655143E-07,-0.613013E-08, 0.169207E-09, 0.301125E-04,-0.461920E-04, 0.871485E-05,-0.622331E-06, 0.151800E-07,-0.478023E-04, 0.247530E-04,-0.381763E-05, 0.232819E-06,-0.494487E-08,-0.336230E-04, 0.223822E-04,-0.384583E-05, 0.252867E-06,-0.572599E-08, 0.105335E-04,-0.567074E-06,-0.216564E-06, 0.237268E-07,-0.658131E-09, 0.282025E-05,-0.671965E-06, 0.565858E-07,-0.193843E-08, 0.211839E-10, 0.157544E-04,-0.304104E-05,-0.624410E-06, 0.120124E-06,-0.457445E-08,-0.188222E-05,-0.407118E-06, 0.375106E-06,-0.466881E-07, 0.158312E-08, 0.945037E-07, 0.564718E-07,-0.319231E-07, 0.371926E-08,-0.123111E-09};
494  static const double xi=2.10, fbeta=1.00, vl=0.001;
495  #endif
496 
497  double BCUT=10000.; // energy up to which soft bremsstrahlung energy loss is calculated
498 
499  double THIGH=100., CHIGH=50.;
500  double dedxBrems=0.;
501 
502  if(BCUT>0.){
503  double T, kc;
504 
505  if(BCUT>=mom) BCUT=mom; // confine BCUT to mom
506 
507  // T=mom, confined to THIGH
508  // kc=BCUT, confined to CHIGH ??
509  if(mom>=THIGH) {
510  T=THIGH;
511  if(BCUT>=THIGH) kc=CHIGH;
512  else kc=BCUT;
513  }
514  else {
515  T=mom;
516  kc=BCUT;
517  }
518 
519  double E=T+me; // total electron energy
520  if(BCUT>T) kc=T;
521 
522  double X=log(T/me);
523  double Y=log(kc/(E*vl));
524 
525  double XX;
526  int K;
527  double S=0., YY=1.;
528 
529  for (unsigned int I=1; I<=2; ++I) {
530  XX=1.;
531  for (unsigned int J=1; J<=6; ++J) {
532  K=6*I+J-6;
533  S=S+C[K]*XX*YY;
534  XX=XX*X;
535  }
536  YY=YY*Y;
537  }
538 
539  for (unsigned int I=3; I<=6; ++I) {
540  XX=1.;
541  for (unsigned int J=1; J<=6; ++J) {
542  K=6*I+J-6;
543  if(Y<=0.) S=S+C[K]*XX*YY;
544  else S=S+C[K+24]*XX*YY;
545  XX=XX*X;
546  }
547  YY=YY*Y;
548  }
549 
550  double SS=0.;
551  YY=1.;
552 
553  for (unsigned int I=1; I<=2; ++I) {
554  XX=1.;
555  for (unsigned int J=1; J<=5; ++J) {
556  K=5*I+J+55;
557  SS=SS+C[K]*XX*YY;
558  XX=XX*X;
559  }
560  YY=YY*Y;
561  }
562 
563  for (unsigned int I=3; I<=5; ++I) {
564  XX=1.;
565  for (unsigned int J=1; J<=5; ++J) {
566  K=5*I+J+55;
567  if(Y<=0.) SS=SS+C[K]*XX*YY;
568  else SS=SS+C[K+15]*XX*YY;
569  XX=XX*X;
570  }
571  YY=YY*Y;
572  }
573 
574  S=S+fmatZ*SS;
575 
576  if(S>0.){
577  double CORR=1.;
578  #if !defined(BETHE)
579  CORR=1./(1.+0.805485E-10*fmatDensity*fmatZ*E*E/(fmatA*kc*kc)); // MIGDAL correction factor
580  #endif
581 
582  double FAC=fmatZ*(fmatZ+xi)*E*E * pow((kc*CORR/T),beta) / (E+me);
583  if(FAC<=0.) return 0.;
584  dedxBrems=FAC*S;
585 
586  double RAT;
587 
588  if(mom>THIGH) {
589  if(BCUT<THIGH) {
590  RAT=BCUT/mom;
591  S=(1.-0.5*RAT+2.*RAT*RAT/9.);
592  RAT=BCUT/T;
593  S=S/(1.-0.5*RAT+2.*RAT*RAT/9.);
594  }
595  else {
596  RAT=BCUT/mom;
597  S=BCUT*(1.-0.5*RAT+2.*RAT*RAT/9.);
598  RAT=kc/T;
599  S=S/(kc*(1.-0.5*RAT+2.*RAT*RAT/9.));
600  }
601  dedxBrems=dedxBrems*S; // GeV barn
602  }
603 
604  dedxBrems = 0.60221367*fmatDensity*dedxBrems/fmatA; // energy loss dE/dx [GeV/cm]
605  }
606  }
607 
608  if (dedxBrems<0.) dedxBrems = 0;
609 
610  double factor=1.; // positron correction factor
611 
612  if (fpdg==-11){
613  static const double AA=7522100., A1=0.415, A3=0.0021, A5=0.00054;
614 
615  double ETA=0.;
616  if(fmatZ>0.) {
617  double X=log(AA*mom/fmatZ*fmatZ);
618  if(X>-8.) {
619  if(X>=+9.) ETA=1.;
620  else {
621  double W=A1*X+A3*pow(X,3.)+A5*pow(X,5.);
622  ETA=0.5+atan(W)/M_PI;
623  }
624  }
625  }
626 
627  double E0;
628 
629  if(ETA<0.0001) factor=1.E-10;
630  else if (ETA>0.9999) factor=1.;
631  else {
632  E0=BCUT/mom;
633  if(E0>1.) E0=1.;
634  if(E0<1.E-8) factor=1.;
635  else factor = ETA * ( 1.-pow(1.-E0, 1./ETA) ) / E0;
636  }
637  }
638 
639  double DE = fstep * factor*dedxBrems; //always positive
640  double momLoss = sqrt(mom*mom+2.*sqrt(mom*mom+fmass*fmass)*DE+DE*DE) - mom; //always positive
641 
642  return momLoss;
643 }
pionana::beta
double beta(double KE, const simb::MCParticle *part)
Definition: TruthAnalyzer_module.cc:59
genie::utils::mec::J
double J(double q0, double q3, double Enu, double ml)
Definition: MECUtils.cxx:147
cet::pow
constexpr T pow(T x)
Definition: pow.h:72
S
Definition: 044_section.h:5
util::kc
constexpr double kc
Speed of light in vacuum in LArSoft units [cm/ns].
Definition: PhysicalConstants.h:59
dump_to_simple_cpp.W
W
Definition: dump_to_simple_cpp.py:43
M_PI
#define M_PI
Definition: includeROOT.h:54
genf::GFMaterialEffects * genf::GFMaterialEffects::getInstance ( )
static

Definition at line 76 of file GFMaterialEffects.cxx.

76  {
77  if(finstance == NULL) finstance = new GFMaterialEffects();
78  return finstance;
79 }
genf::GFMaterialEffects::finstance
static GFMaterialEffects * finstance
Definition: GFMaterialEffects.h:55
void genf::GFMaterialEffects::getParameters ( )
private

contains energy loss classes

interface to material and geometry

Definition at line 255 of file GFMaterialEffects.cxx.

255  {
256  if (!gGeoManager->GetCurrentVolume()->GetMedium())
257  throw GFException(std::string(__func__) + ": no medium", __LINE__, __FILE__).setFatal();
258  TGeoMaterial * mat = gGeoManager->GetCurrentVolume()->GetMedium()->GetMaterial();
259  fmatDensity = mat->GetDensity();
260  fmatZ = mat->GetZ();
261  fmatA = mat->GetA();
262  fradiationLength = mat->GetRadLen();
263  fmEE = MeanExcEnergy_get(mat);
264 
265  // You know what? F*ck it. Just force this to be LAr.... is what I *could/will* say here ....
266  // See comment in energyLossBetheBloch() for why fmEE is in eV here.
267  fmatDensity = 1.40; fmatZ = 18.0; fmatA = 39.95; fradiationLength=13.947; fmEE=188.0;
268 
269 
270  TParticlePDG * part = TDatabasePDG::Instance()->GetParticle(fpdg);
271  fcharge = part->Charge()/(3.);
272  fmass = part->Mass();
273 }
string
std::string string
Definition: nybbler.cc:12
GFException
Exception class for error handling in GENFIT (provides storage for diagnostic information) ...
Definition: GFException.h:48
double genf::GFMaterialEffects::MeanExcEnergy_get ( int  Z)
private

Definition at line 670 of file GFMaterialEffects.cxx.

670  {
671  if ((Z < 0) || (Z > MeanExcEnergy_NELEMENTS))
672  throw GFException(std::string(__func__) + ": unsupported Z", __LINE__, __FILE__).setFatal();
673  return MeanExcEnergy_vals[Z];
674 }
MeanExcEnergy_NELEMENTS
const int MeanExcEnergy_NELEMENTS
Definition: GFMaterialEffects.cxx:667
string
std::string string
Definition: nybbler.cc:12
MeanExcEnergy_vals
const float MeanExcEnergy_vals[MeanExcEnergy_NELEMENTS]
Definition: GFMaterialEffects.cxx:668
GFException
Exception class for error handling in GENFIT (provides storage for diagnostic information) ...
Definition: GFException.h:48
GFException::setFatal
GFException & setFatal(bool b=true)
set fatal flag. if this is true, the fit stops for this current track repr.
Definition: GFException.h:78
double genf::GFMaterialEffects::MeanExcEnergy_get ( TGeoMaterial *  mat)
private

Definition at line 676 of file GFMaterialEffects.cxx.

676  {
677  if(mat->IsMixture()){
678  double logMEE = 0.;
679  double denom = 0.;
680  TGeoMixture *mix = (TGeoMixture*)mat;
681  for(int i=0;i<mix->GetNelements();++i){
682  int index = int(floor((mix->GetZmixt())[i]));
683  logMEE += 1./(mix->GetAmixt())[i]*(mix->GetWmixt())[i]*(mix->GetZmixt())[i]*log(MeanExcEnergy_get(index));
684  denom += (mix->GetWmixt())[i]*(mix->GetZmixt())[i]*1./(mix->GetAmixt())[i];
685  }
686  logMEE/=denom;
687  return exp(logMEE);
688  }
689  else{ // not a mixture
690  int index = int(floor(mat->GetZ()));
691  return MeanExcEnergy_get(index);
692  }
693 }
keras_to_tensorflow.int
int
Definition: keras_to_tensorflow.py:69
void genf::GFMaterialEffects::noiseBetheBloch ( const double &  mom,
TMatrixT< double > *  noise 
) const
private

calculation of energy loss straggling

For the energy loss straggeling, different formulas are used for different regions:

  • Vavilov-Gaussian regime
  • Urban/Landau approximation
  • truncated Landau distribution
  • Urban model

Needs fdedx, which is calculated in energyLossBetheBloch, so it has to be calles afterwards!

Definition at line 327 of file GFMaterialEffects.cxx.

328  {
329 
330 
331  // ENERGY LOSS FLUCTUATIONS; calculate sigma^2(E);
332  double sigma2E = 0.;
333  double zeta = 153.4E3 * fcharge*fcharge/(fbeta*fbeta) * fmatZ/fmatA * fmatDensity * fstep; // eV
334  double Emax = 2.E9*me*fbeta*fbeta*fgammaSquare / (1. + 2.*fgamma*me/fmass + (me/fmass)*(me/fmass) ); // eV
335  double kappa = zeta/Emax;
336 
337  if (kappa > 0.01) { // Vavilov-Gaussian regime
338  sigma2E += zeta*Emax*(1.-fbeta*fbeta/2.); // eV^2
339  }
340  else { // Urban/Landau approximation
341  double alpha = 0.996;
342  double sigmaalpha = 15.76;
343  // calculate number of collisions Nc
344  double I = 16. * pow(fmatZ, 0.9); // eV
345  double f2 = 0.;
346  if (fmatZ > 2.) f2 = 2./fmatZ;
347  double f1 = 1. - f2;
348  double e2 = 10.*fmatZ*fmatZ; // eV
349  double e1 = pow( (I/pow(e2,f2)), 1./f1); // eV
350 
351  double mbbgg2 = 2.E9*fmass*fbeta*fbeta*fgammaSquare; // eV
352  double Sigma1 = fdedx*1.0E9 * f1/e1 * (log(mbbgg2 / e1) - fbeta*fbeta) / (log(mbbgg2 / I) - fbeta*fbeta) * 0.6; // 1/cm
353  double Sigma2 = fdedx*1.0E9 * f2/e2 * (log(mbbgg2 / e2) - fbeta*fbeta) / (log(mbbgg2 / I) - fbeta*fbeta) * 0.6; // 1/cm
354  double Sigma3 = fdedx*1.0E9 * Emax / ( I*(Emax+I)*log((Emax+I)/I) ) * 0.4; // 1/cm
355 
356  double Nc = (Sigma1 + Sigma2 + Sigma3)*fstep;
357 
358  if (Nc > 50.) { // truncated Landau distribution
359  // calculate sigmaalpha (see GEANT3 manual W5013)
360  double RLAMED = -0.422784 - fbeta*fbeta - log(zeta/Emax);
361  double RLAMAX = 0.60715 + 1.1934*RLAMED +(0.67794 + 0.052382*RLAMED)*exp(0.94753+0.74442*RLAMED);
362  // from lambda max to sigmaalpha=sigma (empirical polynomial)
363  if(RLAMAX <= 1010.) {
364  sigmaalpha = 1.975560
365  +9.898841e-02 *RLAMAX
366  -2.828670e-04 *RLAMAX*RLAMAX
367  +5.345406e-07 *pow(RLAMAX,3.)
368  -4.942035e-10 *pow(RLAMAX,4.)
369  +1.729807e-13 *pow(RLAMAX,5.);
370  }
371  else { sigmaalpha = 1.871887E+01 + 1.296254E-02 *RLAMAX; }
372  // alpha=54.6 corresponds to a 0.9996 maximum cut
373  if(sigmaalpha > 54.6) sigmaalpha=54.6;
374  sigma2E += sigmaalpha*sigmaalpha * zeta*zeta; // eV^2
375  }
376  else { // Urban model
377  double Ealpha = I / (1.-(alpha*Emax/(Emax+I))); // eV
378  double meanE32 = I*(Emax+I)/Emax * (Ealpha-I); // eV^2
379  sigma2E += fstep * (Sigma1*e1*e1 + Sigma2*e2*e2 + Sigma3*meanE32); // eV^2
380  }
381  }
382 
383  sigma2E*=1.E-18; // eV -> GeV
384 
385  // update noise matrix
386  (*noise)[6][6] += (mom*mom+fmass*fmass)/pow(mom,6.)*sigma2E;
387 }
reco_momentum_tuples.f2
f2
Definition: reco_momentum_tuples.py:79
cet::pow
constexpr T pow(T x)
Definition: pow.h:72
alpha
double alpha
Definition: doAna.cpp:15
reco_momentum_tuples.f1
f1
Definition: reco_momentum_tuples.py:78
void genf::GFMaterialEffects::noiseBrems ( const double &  mom,
TMatrixT< double > *  noise 
) const
private

calculation of energy loss straggeling

Can be called with any pdg, but only calculates straggeling for electrons and positrons.

Definition at line 646 of file GFMaterialEffects.cxx.

647  {
648 
649  if (fabs(fpdg)!=11) return; // only for electrons and positrons
650 
651  double LX = 1.442695*fstep/fradiationLength;
652  double S2B = mom*mom * ( 1./pow(3.,LX) - 1./pow(4.,LX) );
653  double DEDXB = pow(fabs(S2B),0.5);
654  DEDXB = 1.2E9*DEDXB; //eV
655  double sigma2E = DEDXB*DEDXB; //eV^2
656  sigma2E*=1.E-18; // eV -> GeV
657 
658  (*noise)[6][6] += (mom*mom+fmass*fmass)/pow(mom,6.)*sigma2E;
659 }
cet::pow
constexpr T pow(T x)
Definition: pow.h:72
void genf::GFMaterialEffects::noiseCoulomb ( const double &  mom,
TMatrixT< double > *  noise,
const TMatrixT< double > *  jacobian,
const TVector3 *  directionBefore,
const TVector3 *  directionAfter 
) const
private

calculation of multiple scattering

With the calculated multiple scattering angle, two noise matrices are calculated:

  • with respect to #directionBefore: #noiseBefore, which is then propagated with the jacobian
  • with respect to #directionAfter: #noiseAfter The mean value of these two matrices is added to the noise matrix #noise. This method gives better results than either calculating only noiseBefore or noiseAfter.

    This is a detailed description of the mathematics involved:
    We define a local coordinate system cs' with initial momentum in z-direction:

    \[ \left(\begin{array}{c} x'\\ y'\\ z'\\ a_{x}'\\ a_{y}'\\ a_{z}'\\ \frac{q}{p}'\end{array}\right)=\left(\begin{array}{ccccccc} \cos\psi & \sin\psi & 0\\ -\cos\vartheta\sin\psi & \cos\vartheta\cos\psi & \sin\psi\\ \sin\vartheta\sin\psi & -\sin\vartheta\cos\psi & \cos\vartheta\\ & & & \cos\psi & \sin\psi & 0\\ & & & -\cos\vartheta\sin\psi & \cos\vartheta\cos\psi & \sin\psi\\ & & & \sin\vartheta\sin\psi & -\sin\vartheta\cos\psi & \cos\vartheta\\ & & & & & & 1\end{array}\right)\left(\begin{array}{c} x\\ y\\ z\\ a_{x}\\ a_{y}\\ a_{z}\\ \frac{q}{p}\end{array}\right)=R^{T}\left(\begin{array}{c} x\\ y\\ z\\ a_{x}\\ a_{y}\\ a_{z}\\ \frac{q}{p}\end{array}\right)\]


Now the global coordinate system cs is:

\[ \left(\begin{array}{c} x\\ y\\ z\\ a_{x}\\ a_{y}\\ a_{z}\\ \frac{q}{p}\end{array}\right)=\left(\begin{array}{ccccccc} \cos\psi & -\cos\vartheta\sin\psi & \sin\vartheta\sin\psi\\ \sin\psi & \cos\vartheta\cos\psi & -\sin\vartheta\cos\psi\\ 0 & \sin\psi & \cos\vartheta\\ & & & \cos\psi & -\cos\vartheta\sin\psi & \sin\vartheta\sin\psi\\ & & & \sin\psi & \cos\vartheta\cos\psi & -\sin\vartheta\cos\psi\\ & & & 0 & \sin\psi & \cos\vartheta\\ & & & & & & 1\end{array}\right)\left(\begin{array}{c} x'\\ y'\\ z'\\ a_{x}'\\ a_{y}'\\ a_{z}'\\ \frac{q}{p}'\end{array}\right)=R\left(\begin{array}{c} x'\\ y'\\ z'\\ a_{x}'\\ a_{y}'\\ a_{z}'\\ \frac{q}{p}'\end{array}\right) \]


with the Euler angles

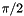
\begin{eqnarray*} \psi & = & \begin{cases} \begin{cases} \frac{\pi}{2} & a_{x} \geq 0 \\ \frac{3\pi}{2} & a_{x} < 0 \end{cases} & a_{y}=0 \mbox{ resp. } |a_{y}|<10^{-14} \\ - \arctan \frac{a_{x}}{a_{y}} & a_{y} < 0 \\ \pi - \arctan \frac{a_{x}}{a_{y}} & a_{y} > 0 \end{cases} \\ \vartheta & = & \arccos a_{z} \end{eqnarray*}


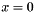$M$ is the multiple scattering error-matrix in the 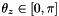$\theta$ coordinate system. 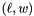$\theta_{1/2}=0$ are the multiple scattering angles. There is only an error in direction (which later leads to an error in position, when 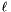$N_{before}$ is propagated with $T$).

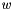\[ M=\left(\begin{array}{cc} \sigma^{2} & 0\\ 0 & \sigma^{2}\end{array}\right)\]


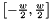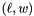This translates into the noise matrix $\overline{M}$ in the local cs' via jacobian J. The mean scattering angle is always 0, this means that $\theta_{1/2}=0$):

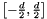
\begin{eqnarray*} x' & = & x'\\ y' & = & y'\\ z' & = & z'\\ a_{x}' & = & \sin\theta_{1}\\ a_{y}' & = & \sin\theta_{2}\\ a_{z}' & = & \sqrt{1-\sin^{2}\theta_{1}-\sin^{2}\theta_{2}}\\ \frac{q}{p}' & = & \frac{q}{p}'\end{eqnarray*}

\[ M=\left(\begin{array}{cc} \sigma^{2} & 0\\ 0 & \sigma^{2}\end{array}\right)\]


\[ J=\frac{\partial\left(x',y',z',a_{x}',a_{y}',a_{z}',\frac{q}{p}'\right)}{\partial\left(\theta_{1},\theta_{2}\right)}\]


\[ J=\left(\begin{array}{cc} 0 & 0\\ 0 & 0\\ 0 & 0\\ \cos\theta_{1} & 0\\ 0 & \cos\theta_{2}\\ -\frac{\cos\theta_{1}\sin\theta_{1}}{\sqrt{\cos^{2}\theta_{1}-\sin^{2}\theta_{2}}} & -\frac{\cos\theta_{2}\sin\theta_{2}}{\sqrt{\cos^{2}\theta_{1}-\sin^{2}\theta_{2}}}\\ 0 & 0\end{array}\right) \overset{\theta_{1/2}=0}{=} \left(\begin{array}{cc} 0 & 0\\ 0 & 0\\ 0 & 0\\ 1 & 0\\ 0 & 1\\ 0 & 0\\ 0 & 0\end{array}\right)\]


\[ \overline{M}=J\: M\: J^{T}=\left(\begin{array}{ccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & \sigma^{2} & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & \sigma^{2} & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right)\]

The following transformation brings the noise matrix into the global coordinate system cs, resulting in 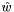$N$ :

\[ N=R\overline{M}R^{T}=\sigma^{2}\left(\begin{array}{ccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & \cos^{2}\psi+\cos^{2}\theta-\cos^{2}\theta\cos^{2}\psi & \cos\psi\sin\psi\sin^{2}\theta & -\cos\theta\sin\psi\sin\theta & 0\\ 0 & 0 & 0 & \cos\psi\sin\psi\sin^{2}\theta & \sin^{2}\psi+\cos^{2}\theta\cos^{2}\psi & \cos\theta\cos\psi\sin\theta & 0\\ 0 & 0 & 0 & -\cos\theta\sin\psi\sin\theta & \cos\theta\cos\psi\sin\theta & \sin^{2}\theta & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right)\]


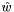Now two $N$ are calculated: 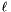$N_{before}$ (at the start point, with initial direction #directionBefore) and 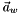$N_{after}$ (at the final point, with direction #directionAfter). 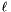$N_{before}$ is the propagated with the #jacobian of extrapolation 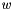$T$. The new covariance matrix with multiple scattering in global cs is:

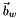
\begin{eqnarray*} C_{new} & = C_{old} + 0.5 \cdot T N_{before} T^{T} + 0.5 \cdot N_{after} \end{eqnarray*}



See also: Track following in dense media and inhomogeneous magnetic fields, A.Fontana, P.Genova, L.Lavezzi and A.Rotondi; PANDA Report PV/01-07

Definition at line 390 of file GFMaterialEffects.cxx.

394  {
395 
396  // MULTIPLE SCATTERING; calculate sigma^2
397  // PANDA report PV/01-07 eq(43); linear in step length
398  double sigma2 = 225.E-6/(fbeta*fbeta*mom*mom) * fstep/fradiationLength * fmatZ/(fmatZ+1) * log(159.*pow(fmatZ,-1./3.))/log(287.*pow(fmatZ,-0.5)); // sigma^2 = 225E-6/mom^2 * XX0/fbeta^2 * Z/(Z+1) * ln(159*Z^(-1/3))/ln(287*Z^(-1/2)
399 
400  // noiseBefore
401  TMatrixT<double> noiseBefore(7,7);
402 
403  // calculate euler angles theta, psi (so that directionBefore' points in z' direction)
404  double psi = 0;
405  if (fabs((*directionBefore)[1]) < 1E-14) { // numerical case: arctan(+-inf)=+-PI/2
406  if ((*directionBefore)[0] >= 0.) psi = M_PI/2.;
407  else psi = 3.*M_PI/2.;
408  }
409  else {
410  if ((*directionBefore)[1] > 0.) psi = M_PI - atan((*directionBefore)[0]/(*directionBefore)[1]);
411  else psi = -atan((*directionBefore)[0]/(*directionBefore)[1]);
412  }
413  // cache sin and cos
414  double sintheta = sqrt(1-(*directionBefore)[2]*(*directionBefore)[2]); // theta = arccos(directionBefore[2])
415  double costheta = (*directionBefore)[2];
416  double sinpsi = sin(psi);
417  double cospsi = cos(psi);
418 
419  // calculate NoiseBefore Matrix R M R^T
420  double noiseBefore34 = sigma2 * cospsi * sinpsi * sintheta*sintheta; // noiseBefore_ij = noiseBefore_ji
421  double noiseBefore35 = -sigma2 * costheta * sinpsi * sintheta;
422  double noiseBefore45 = sigma2 * costheta * cospsi * sintheta;
423 
424  noiseBefore[3][3] = sigma2 * (cospsi*cospsi + costheta*costheta - costheta*costheta * cospsi*cospsi);
425  noiseBefore[4][3] = noiseBefore34;
426  noiseBefore[5][3] = noiseBefore35;
427 
428  noiseBefore[3][4] = noiseBefore34;
429  noiseBefore[4][4] = sigma2 * (sinpsi*sinpsi + costheta*costheta * cospsi*cospsi);
430  noiseBefore[5][4] = noiseBefore45;
431 
432  noiseBefore[3][5] = noiseBefore35;
433  noiseBefore[4][5] = noiseBefore45;
434  noiseBefore[5][5] = sigma2 * sintheta*sintheta;
435 
436  TMatrixT<double> jacobianT(7,7);
437  jacobianT = (*jacobian);
438  jacobianT.T();
439 
440  noiseBefore = jacobianT*noiseBefore*(*jacobian); //propagate
441 
442  // noiseAfter
443  TMatrixT<double> noiseAfter(7,7);
444 
445  // calculate euler angles theta, psi (so that A' points in z' direction)
446  psi = 0;
447  if (fabs((*directionAfter)[1]) < 1E-14) { // numerical case: arctan(+-inf)=+-PI/2
448  if ((*directionAfter)[0] >= 0.) psi = M_PI/2.;
449  else psi = 3.*M_PI/2.;
450  }
451  else {
452  if ((*directionAfter)[1] > 0.) psi = M_PI - atan((*directionAfter)[0]/(*directionAfter)[1]);
453  else psi = -atan((*directionAfter)[0]/(*directionAfter)[1]);
454  }
455  // cache sin and cos
456  sintheta = sqrt(1-(*directionAfter)[2]*(*directionAfter)[2]); // theta = arccos(directionAfter[2])
457  costheta = (*directionAfter)[2];
458  sinpsi = sin(psi);
459  cospsi = cos(psi);
460 
461  // calculate NoiseAfter Matrix R M R^T
462  double noiseAfter34 = sigma2 * cospsi * sinpsi * sintheta*sintheta; // noiseAfter_ij = noiseAfter_ji
463  double noiseAfter35 = -sigma2 * costheta * sinpsi * sintheta;
464  double noiseAfter45 = sigma2 * costheta * cospsi * sintheta;
465 
466  noiseAfter[3][3] = sigma2 * (cospsi*cospsi + costheta*costheta - costheta*costheta * cospsi*cospsi);
467  noiseAfter[4][3] = noiseAfter34;
468  noiseAfter[5][3] = noiseAfter35;
469 
470  noiseAfter[3][4] = noiseAfter34;
471  noiseAfter[4][4] = sigma2 * (sinpsi*sinpsi + costheta*costheta * cospsi*cospsi);
472  noiseAfter[5][4] = noiseAfter45;
473 
474  noiseAfter[3][5] = noiseAfter35;
475  noiseAfter[4][5] = noiseAfter45;
476  noiseAfter[5][5] = sigma2 * sintheta*sintheta;
477 
478  //calculate mean of noiseBefore and noiseAfter and update noise
479  (*noise) += 0.5*noiseBefore + 0.5*noiseAfter;
480 
481 }
cet::pow
constexpr T pow(T x)
Definition: pow.h:72
M_PI
#define M_PI
Definition: includeROOT.h:54
void genf::GFMaterialEffects::setEnergyLossBetheBloch ( bool  opt = true)
inline

Definition at line 61 of file GFMaterialEffects.h.

61 {fEnergyLossBetheBloch=opt;}
train.opt
opt
Definition: train.py:196
void genf::GFMaterialEffects::setEnergyLossBrems ( bool  opt = true)
inline

Definition at line 64 of file GFMaterialEffects.h.

64 {fEnergyLossBrems=opt;}
train.opt
opt
Definition: train.py:196
void genf::GFMaterialEffects::setNoiseBetheBloch ( bool  opt = true)
inline

Definition at line 62 of file GFMaterialEffects.h.

62 {fNoiseBetheBloch=opt;}
train.opt
opt
Definition: train.py:196
void genf::GFMaterialEffects::setNoiseBrems ( bool  opt = true)
inline

Definition at line 65 of file GFMaterialEffects.h.

65 {fNoiseBrems=opt;}
train.opt
opt
Definition: train.py:196
void genf::GFMaterialEffects::setNoiseCoulomb ( bool  opt = true)
inline

Definition at line 63 of file GFMaterialEffects.h.

63 {fNoiseCoulomb=opt;}
train.opt
opt
Definition: train.py:196
double genf::GFMaterialEffects::stepper ( const double &  maxDist,
const double &  posx,
const double &  posy,
const double &  posz,
const double &  dirx,
const double &  diry,
const double &  dirz,
const double &  mom,
const int &  pdg 
)

Returns maximum length so that a specified momentum loss will not be exceeded.

The stepper returns the maximum length that the particle may travel, so that a specified relative momentum loss will not be exceeded.

Definition at line 183 of file GFMaterialEffects.cxx.

191  {
192 
193  static const double maxPloss = .005; // maximum relative momentum loss allowed
194 
195  gGeoManager->InitTrack(posx,posy,posz,dirx,diry,dirz);
196 
197  double X(0.);
198  double dP = 0.;
199  double momLoss = 0.;
200  /*
201  double matDensity, matZ, matA, radiationLength, mEE;
202  double step;
203  */
204 
205  while(X<maxDist){
206 
207  getParameters();
208 
209  gGeoManager->FindNextBoundaryAndStep(maxDist-X);
210  fstep = gGeoManager->GetStep();
211  //
212  // step = geoMatManager->stepOrNextBoundary(maxDist-X);
213 
214  // Loop over EnergyLoss classes
215 
216  if(fmatZ>1.E-3){
217  /*
218  for(unsigned int j=0;j<fEnergyLoss.size();++j){
219  momLoss += fEnergyLoss.at(j)->energyLoss(step,
220  mom,
221  pdg,
222  matDensity,
223  matZ,
224  matA,
225  radiationLength,
226  mEE);
227  }
228  */
229  calcBeta(mom);
230 
231  if (fEnergyLossBetheBloch)
232  momLoss += this->energyLossBetheBloch(mom);
233 
234  if (fEnergyLossBrems)
235  momLoss += this->energyLossBrems(mom);
236 
237  }
238 
239  if(dP + momLoss > mom*maxPloss){
240  double fraction = (mom*maxPloss-dP)/momLoss;
241  if ((fraction <= 0.) || (fraction >= 1.))
242  throw GFException(std::string(__func__) + ": invalid fraction", __LINE__, __FILE__).setFatal();
243  dP+=fraction*momLoss;
244  X+=fraction*fstep;
245  break;
246  }
247 
248  dP += momLoss;
249  X += fstep;
250  }
251 
252  return X;
253 }
string
std::string string
Definition: nybbler.cc:12
genf::GFMaterialEffects::energyLossBrems
double energyLossBrems(const double &mom) const
Returns energy loss.
Definition: GFMaterialEffects.cxx:484
genf::GFMaterialEffects::calcBeta
void calcBeta(double mom)
sets fbeta, fgamma, fgammasquare; must only be used after calling getParameters() ...
Definition: GFMaterialEffects.cxx:276
GFException
Exception class for error handling in GENFIT (provides storage for diagnostic information) ...
Definition: GFException.h:48
genf::GFMaterialEffects::getParameters
void getParameters()
contains energy loss classes
Definition: GFMaterialEffects.cxx:255
genf::GFMaterialEffects::energyLossBetheBloch
double energyLossBetheBloch(const double &mom)
Returns energy loss.
Definition: GFMaterialEffects.cxx:290
double genf::GFMaterialEffects::stepper ( const double &  maxDist,
const TVector3 &  pos,
const TVector3 &  dir,
const double &  mom,
const int &  pdg 
)
inline

Definition at line 90 of file GFMaterialEffects.h.

94  {
95  return stepper(maxDist, pos.X(),pos.Y(),pos.Z(),dir.X(),dir.Y(),dir.Z(),mom,pdg);};
dir
string dir
Definition: INukeNucleonCorr.cxx:61
run_cnn_1class.pdg
pdg
Definition: run_cnn_1class.py:54
genf::GFMaterialEffects::stepper
double stepper(const double &maxDist, const double &posx, const double &posy, const double &posz, const double &dirx, const double &diry, const double &dirz, const double &mom, const int &pdg)
Returns maximum length so that a specified momentum loss will not be exceeded.
Definition: GFMaterialEffects.cxx:183

Member Data Documentation

double genf::GFMaterialEffects::fbeta
private

Definition at line 350 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fcharge
private

Definition at line 362 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fdedx
private

Definition at line 351 of file GFMaterialEffects.h.

bool genf::GFMaterialEffects::fEnergyLossBetheBloch
private

Definition at line 339 of file GFMaterialEffects.h.

bool genf::GFMaterialEffects::fEnergyLossBrems
private

Definition at line 342 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fgamma
private

Definition at line 352 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fgammaSquare
private

Definition at line 353 of file GFMaterialEffects.h.

genf::GFMaterialEffects * genf::GFMaterialEffects::finstance = NULL
staticprivate

Definition at line 55 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fmass
private

Definition at line 363 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fmatA
private

Definition at line 357 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fmatDensity
private

Definition at line 355 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fmatZ
private

Definition at line 356 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fmEE
private

Definition at line 359 of file GFMaterialEffects.h.

bool genf::GFMaterialEffects::fNoiseBetheBloch
private

Definition at line 340 of file GFMaterialEffects.h.

bool genf::GFMaterialEffects::fNoiseBrems
private

Definition at line 343 of file GFMaterialEffects.h.

bool genf::GFMaterialEffects::fNoiseCoulomb
private

Definition at line 341 of file GFMaterialEffects.h.

int genf::GFMaterialEffects::fpdg
private

Definition at line 361 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fradiationLength
private

Definition at line 358 of file GFMaterialEffects.h.

double genf::GFMaterialEffects::fstep
private

Definition at line 347 of file GFMaterialEffects.h.

const double genf::GFMaterialEffects::me
private

Definition at line 345 of file GFMaterialEffects.h.

The documentation for this class was generated from the following files:
Generated by   doxygen 1.8.11