Abstract interface for an object that computes the elements ( 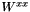 ,
, 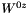 , etc.) and structure functions (
, etc.) and structure functions ( 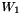 ,
, 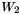 , etc.) of the hadron tensor
, etc.) of the hadron tensor 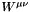 defined according to the conventions of the Valencia model.
More...
defined according to the conventions of the Valencia model.
More...
#include <LabFrameHadronTensorI.h>
Public Member Functions | ||||||||||
| virtual | ~LabFrameHadronTensorI () | |||||||||
| virtual double | contraction (const Interaction *interaction, double Q_value) const | |||||||||
| virtual double | contraction (int probe_pdg, double E_probe, double m_probe, double Tl, double cos_l, double ml, double Q_value) const | |||||||||
| virtual double | dSigma_dT_dCosTheta (const Interaction *interaction, double Q_value) const =0 | |||||||||
| virtual double | dSigma_dT_dCosTheta (int probe_pdg, double E_probe, double m_probe, double Tl, double cos_l, double ml, double Q_value) const =0 | |||||||||
| virtual double | dSigma_dT_dCosTheta_rosenbluth (const Interaction *interaction, double Q_value) const =0 | |||||||||
| virtual double | dSigma_dT_dCosTheta_rosenbluth (int probe_pdg, double E_probe, double m_probe, double Tl, double cos_l, double ml, double Q_value) const =0 | |||||||||
Tensor elements | ||||||||||
Functions that return the elements of the tensor. Since it is Hermitian, only ten elements are independent. Although a return type of std::complex<double> is used for all elements, note that hermiticity implies that the diagonal elements must be real.
| ||||||||||
| virtual std::complex< double > | tx (double, double) const | |||||||||
The tensor element 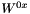 . More... . More... | ||||||||||
| virtual std::complex< double > | ty (double, double) const | |||||||||
The tensor element 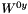 . More... . More... | ||||||||||
| virtual std::complex< double > | xt (double q0, double q_mag) const | |||||||||
The tensor element 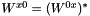 . More... . More... | ||||||||||
| virtual std::complex< double > | xz (double, double) const | |||||||||
The tensor element 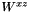 . More... . More... | ||||||||||
| virtual std::complex< double > | yt (double q0, double q_mag) const | |||||||||
The tensor element 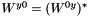 . More... . More... | ||||||||||
| virtual std::complex< double > | yx (double q0, double q_mag) const | |||||||||
The tensor element 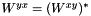 . More... . More... | ||||||||||
| virtual std::complex< double > | yy (double q0, double q_mag) const | |||||||||
The tensor element 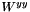 . More... . More... | ||||||||||
| virtual std::complex< double > | yz (double, double) const | |||||||||
The tensor element 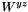 . More... . More... | ||||||||||
| virtual std::complex< double > | zt (double q0, double q_mag) const | |||||||||
The tensor element 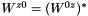 . More... . More... | ||||||||||
| virtual std::complex< double > | zx (double q0, double q_mag) const | |||||||||
The tensor element 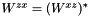 . More... . More... | ||||||||||
| virtual std::complex< double > | zy (double q0, double q_mag) const | |||||||||
The tensor element 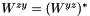 . More... . More... | ||||||||||
Structure functions | ||||||||||
| ||||||||||
| virtual double | W1 (double q0, double q_mag, double Mi) const =0 | |||||||||
The structure function 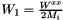 . More... . More... | ||||||||||
| virtual double | W2 (double q0, double q_mag, double Mi) const =0 | |||||||||
| virtual double | W3 (double q0, double q_mag, double Mi) const =0 | |||||||||
| virtual double | W4 (double q0, double q_mag, double Mi) const =0 | |||||||||
| virtual double | W5 (double q0, double q_mag, double Mi) const =0 | |||||||||
| virtual double | W6 (double q0, double q_mag, double Mi) const =0 | |||||||||
 Public Member Functions inherited from genie::HadronTensorI Public Member Functions inherited from genie::HadronTensorI | ||||||||||
| virtual | ~HadronTensorI () | |||||||||
| int | pdg () const | |||||||||
| PDG code of the target nucleus. More... | ||||||||||
| int | Z () const | |||||||||
| Atomic number of the target nucleus. More... | ||||||||||
| int | A () const | |||||||||
| Mass number of the target nucleus. More... | ||||||||||
| void | set_pdg (int pdg) | |||||||||
| Set the target nucleus PDG code. More... | ||||||||||
| virtual double | q0Min () const =0 | |||||||||
| virtual double | q0Max () const =0 | |||||||||
| virtual double | qMagMin () const =0 | |||||||||
| virtual double | qMagMax () const =0 | |||||||||
| virtual std::complex< double > | tt (double q0, double q_mag) const =0 | |||||||||
The tensor element 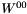 . More... . More... | ||||||||||
| virtual std::complex< double > | tz (double q0, double q_mag) const =0 | |||||||||
The tensor element 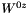 . More... . More... | ||||||||||
| virtual std::complex< double > | xx (double q0, double q_mag) const =0 | |||||||||
The tensor element 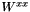 . More... . More... | ||||||||||
| virtual std::complex< double > | xy (double q0, double q_mag) const =0 | |||||||||
The tensor element 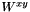 . More... . More... | ||||||||||
| virtual std::complex< double > | zz (double q0, double q_mag) const =0 | |||||||||
The tensor element 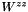 . More... . More... | ||||||||||
Protected Member Functions | |
| LabFrameHadronTensorI (int pdg=0) | |
| LabFrameHadronTensorI (int Z, int A) | |
 Protected Member Functions inherited from genie::HadronTensorI Protected Member Functions inherited from genie::HadronTensorI | |
| HadronTensorI (int pdg=0) | |
| HadronTensorI (int Z, int A) | |
| PDG code for the target nucleus represented by the tensor. More... | |
Additional Inherited Members | |
 Protected Attributes inherited from genie::HadronTensorI Protected Attributes inherited from genie::HadronTensorI | |
| int | fTargetPDG |
Abstract interface for an object that computes the elements ( 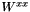 ,
, 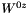 , etc.) and structure functions (
, etc.) and structure functions ( 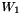 ,
, 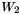 , etc.) of the hadron tensor
, etc.) of the hadron tensor 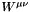 defined according to the conventions of the Valencia model.
defined according to the conventions of the Valencia model.
For (anti)neutrino projectiles, the hadron tensor 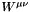 is defined as in equations (8) and (9) of
is defined as in equations (8) and (9) of
J. Nieves, J. E. Amaro, and M. Valverde, "Inclusive Quasi-Elastic Charged-Current Neutrino-Nucleus Reactions," Phys. Rev. C 70, 055503 (2004) https://doi.org/10.1103/PhysRevC.70.055503 https://arxiv.org/abs/nucl-th/0408005v3
Note that the associated erratum includes an important correction in the formula for the differential cross section:
J. Nieves, J. E. Amaro, and M. Valverde, "Erratum: Inclusive quasielastic charged-current neutrino-nucleus reactions [Phys. Rev. C 70, 055503 (2004)]," Phys. Rev. C. 72, 019902 (2005) http://doi.org/10.1103/PhysRevC.72.019902
The calculation is carried out in the lab frame (i.e., the frame where the target nucleus has initial 4-momentum 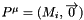 ) with the 3-momentum transfer
) with the 3-momentum transfer 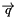 chosen to lie along the z axis, i.e.,
chosen to lie along the z axis, i.e., 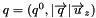 . With this choice of frame, the only nonzero elements are
. With this choice of frame, the only nonzero elements are 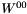 ,
, 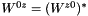 ,
, 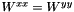 ,
, 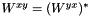 , and
, and 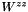 .
.
For an electron projectile, the hadron tensor is defined as in
equation (83) of
A. Gil, J. Nieves, and E. Oset,
"Many-body approach to the inclusive \form#176 reaction
from the quasielastic to the \form#177 excitation region,"
Nuclear Physics A 627, 543-598 (1997)
http://doi.org/10.1016/S0375-9474(97)00513-7
It is evaluated in the same reference frame as the neutrino case.
August 23, 2018
Copyright (c) 2003-2018, The GENIE Collaboration For the full text of the license visit http://copyright.genie-mc.org or see $GENIE/LICENSE
Definition at line 74 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
Definition at line 78 of file LabFrameHadronTensorI.h.
|
inlineprotected |
Definition at line 226 of file LabFrameHadronTensorI.h.
|
inlineprotected |
Definition at line 228 of file LabFrameHadronTensorI.h.
|
virtual |
Computes the contraction 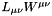 of the hadron tensor with the appropriate lepton tensor for a given type of projectile (e.g., neutrino, electron)
of the hadron tensor with the appropriate lepton tensor for a given type of projectile (e.g., neutrino, electron)
| [in] | interaction | An Interaction object storing information about the initial and final states |
| [in] | Q_value | The Q-value that should be used to correct the energy transfer 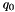 (GeV) (GeV) |
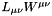 (GeV)
(GeV) Implements genie::HadronTensorI.
Definition at line 11 of file LabFrameHadronTensorI.cxx.
|
virtual |
| [in] | probe_pdg | The PDG code for the incident projectile |
| [in] | E_probe | The lab frame energy of the incident projectile (GeV) |
| [in] | m_probe | The mass of the incident projectile (GeV) |
| [in] | Tl | The lab frame kinetic energy of the final state lepton (GeV) |
| [in] | cos_l | The angle between the direction of the incident neutrino and the final state lepton (radians) |
| [in] | ml | The mass of the final state lepton (GeV) |
| [in] | Q_value | The Q-value that should be used to correct the energy transfer 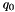 (GeV) (GeV) |
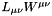 (GeV)
(GeV) See equation (3) of Nieves, Amaro, and Valverde, Phys. Rev. C 70, 055503 (2004)
See equation (82) of Gil, Nieves, and Oset, Nucl. Phys. A 627, 543 (1997)
Definition at line 27 of file LabFrameHadronTensorI.cxx.
|
pure virtual |
Computes the differential cross section 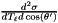 for the reaction represented by this hadron tensor
for the reaction represented by this hadron tensor
| [in] | interaction | An Interaction object storing information about the initial and final states |
| [in] | Q_value | The Q-value that should be used to correct the energy transfer 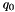 (GeV) (GeV) |
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
| [in] | probe_pdg | The PDG code for the incident projectile |
| [in] | E_probe | The lab frame energy of the incident projectile (GeV) |
| [in] | m_probe | The mass of the incident projectile (GeV) |
| [in] | Tl | The lab frame kinetic energy of the final state lepton (GeV) |
| [in] | cos_l | The angle between the direction of the incident neutrino and the final state lepton (radians) |
| [in] | ml | The mass of the final state lepton (GeV) |
| [in] | Q_value | The Q-value that should be used to correct the energy transfer 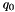 (GeV) (GeV) |
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
Implemented in genie::TabulatedLabFrameHadronTensor.
|
inlinevirtual |
The tensor element 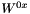 .
.
Implements genie::HadronTensorI.
Definition at line 92 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 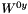 .
.
Implements genie::HadronTensorI.
Definition at line 96 of file LabFrameHadronTensorI.h.
|
pure virtual |
The structure function 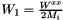 .
.
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
The structure function 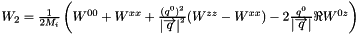
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
The structure function 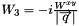
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
The structure function 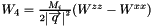
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
The structure function 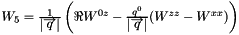
Implemented in genie::TabulatedLabFrameHadronTensor.
|
pure virtual |
The structure function 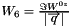
Implemented in genie::TabulatedLabFrameHadronTensor.
|
inlinevirtual |
The tensor element 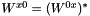 .
.
Implements genie::HadronTensorI.
Definition at line 100 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 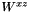 .
.
Implements genie::HadronTensorI.
Definition at line 104 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 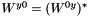 .
.
Implements genie::HadronTensorI.
Definition at line 108 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 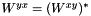 .
.
Implements genie::HadronTensorI.
Definition at line 112 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 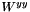 .
.
Implements genie::HadronTensorI.
Definition at line 116 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 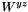 .
.
Implements genie::HadronTensorI.
Definition at line 120 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 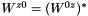 .
.
Implements genie::HadronTensorI.
Definition at line 124 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 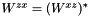 .
.
Implements genie::HadronTensorI.
Definition at line 128 of file LabFrameHadronTensorI.h.
|
inlinevirtual |
The tensor element 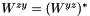 .
.
Implements genie::HadronTensorI.
Definition at line 132 of file LabFrameHadronTensorI.h.
 1.8.11
1.8.11